Pubblicato su Il Sole 24 Ore del 15 Ottobre 2017
Per capire come finiranno le prossime elezioni politiche non servono strumenti complessi o ragionamenti particolarmente sofisticati. Basta una semplice tabella che tenga conto delle regole del voto e degli attori in competizione. Sulle prime deciderà il Senato in settimana. Il Rosatellum-bis pare destinato ad essere definitivamente approvato. Sui secondi sappiamo già quanto ci interessa sapere in questa fase, e cioè il numero. Ci sarà una coalizione di centro-sinistra, una di centro-destra e il M5s. Non conosciamo la composizione delle coalizioni, ma è un dato che non serve per quello che vogliamo dimostrare ora.
Il nuovo sistema elettorale assegnerà alla Camera 232 seggi in altrettanti collegi uninominali con la formula della maggioranza relativa e 386 seggi con formula proporzionale. Per vincere i primi basterà che un candidato ottenga un voto più degli altri. Per ottenere i secondi occorrerà avere almeno il 3% dei voti a livello nazionale. Fuori dal conto restano i 12 seggi della circoscrizione estero che, esclusi dai nostri calcoli, potrebbero comunque essere decisivi per formare un governo dopo il voto. I “Pallaro” (il senatore italo-argentino che sostenne il governo Prodi ma poi contribuì alla sua caduta) del 2018 potrebbero ancora essere una risorsa del sistema.
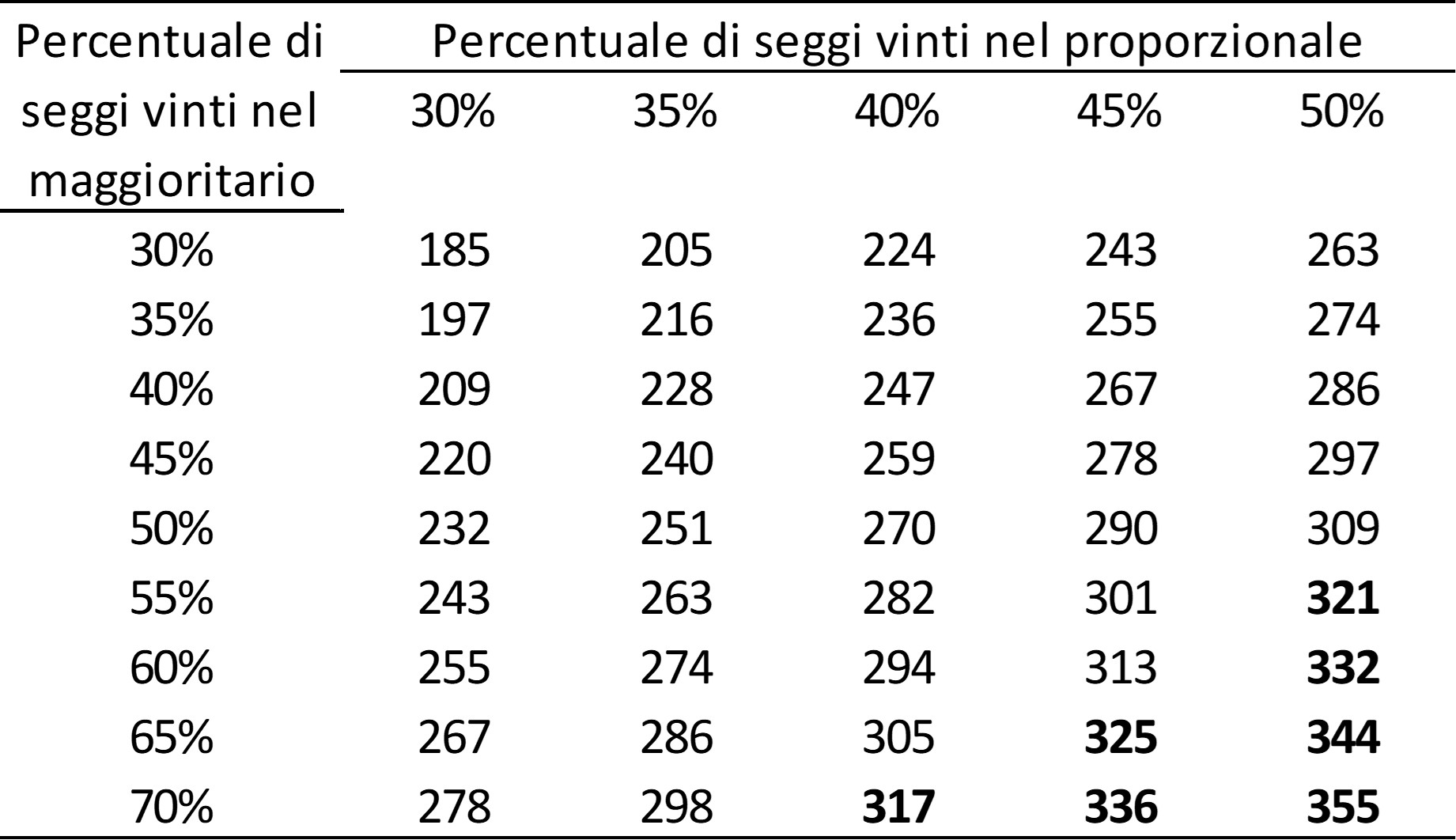
Nella tabella abbiamo fatto una operazione semplicissima. Abbiamo incrociato la percentuale dei 386 seggi proporzionali che un qualunque attore potrebbe ottenere con la percentuale dei 232 seggi maggioritari che lo stesso attore potrebbe vincere nei collegi uninominali. I numeri nelle singole caselle della tabella sono il totale dei seggi che risultano dall’incrocio delle due percentuali. Per esempio, se uno dei tre principali attori della competizione – centro-sinistra, centro-destra o M5s- ottenesse il 35 % dei seggi proporzionali e il 50% dei seggi maggioritari il numero dei suoi deputati sarebbe 251. E così via.
In questo momento noi non sappiamo quanti voti e quanti seggi prenderanno il M5s e ciascuna delle due coalizioni che si presenteranno alle prossime elezioni. Ma pur non conoscendo questo dato la tabella fa vedere con matematica chiarezza che la combinazione di seggi proporzionali e di seggi maggioritari difficilmente produrrà una maggioranza a favore di uno dei contendenti, cioè quei 316 seggi che servono alla Camera per fare il governo. Certo, se ipotizziamo che uno dei tre attori possa conquistare il 50 per cento dei seggi proporzionali e il 70 di quelli maggioritari il gioco sarebbe fatto e non staremmo qui a preoccuparci di come si farà il governo dopo il voto. Ma è realistico che la coalizione di Renzi o quella di Berlusconi oppure il partito di Di Maio possano arrivare a queste percentuali ? La risposta non può che essere negativa.
Ma se anche immaginassimo che uno dei contendenti arrivi al 40 per cento dei seggi proporzionali dovrebbe pur vincere il 70% dei seggi maggioritari per ottenere una maggioranza risicata di 317 seggi totali. Se invece ipotizziamo che uno dei tre competitori vinca il 55 per cento dei seggi maggioritari dovrebbe ottenere la percentuale straordinariamente elevata del 50 per cento dei seggi proporzionali per arrivare a 321 seggi totali. Pur nell’incertezza che caratterizza in questa fase il comportamento degli elettori queste combinazioni appaiono decisamente poco credibili.
E allora la conclusione è ineludibile: il prossimo governo dovrà necessariamente nascere dalla scomposizione delle coalizioni che si presenteranno davanti agli elettori in campagna elettorale e dalla loro ricomposizione in una maggioranza di governo che non corrisponderà alle solenni promesse fatte agli elettori al momento del voto. E tutto ciò sperando che sia possibile assemblare una qualunque maggioranza di governo, viste le preclusioni, i veti e le idiosincrasie dei nostri partiti.
Sarà un brutto spettacolo. Con buona pace di tutti coloro che votando no al referendum del 4 Dicembre 2016 e applaudendo la sentenza della Consulta sull’Italicum del Febbraio 2017 credevano di fare il bene dell’Italia.